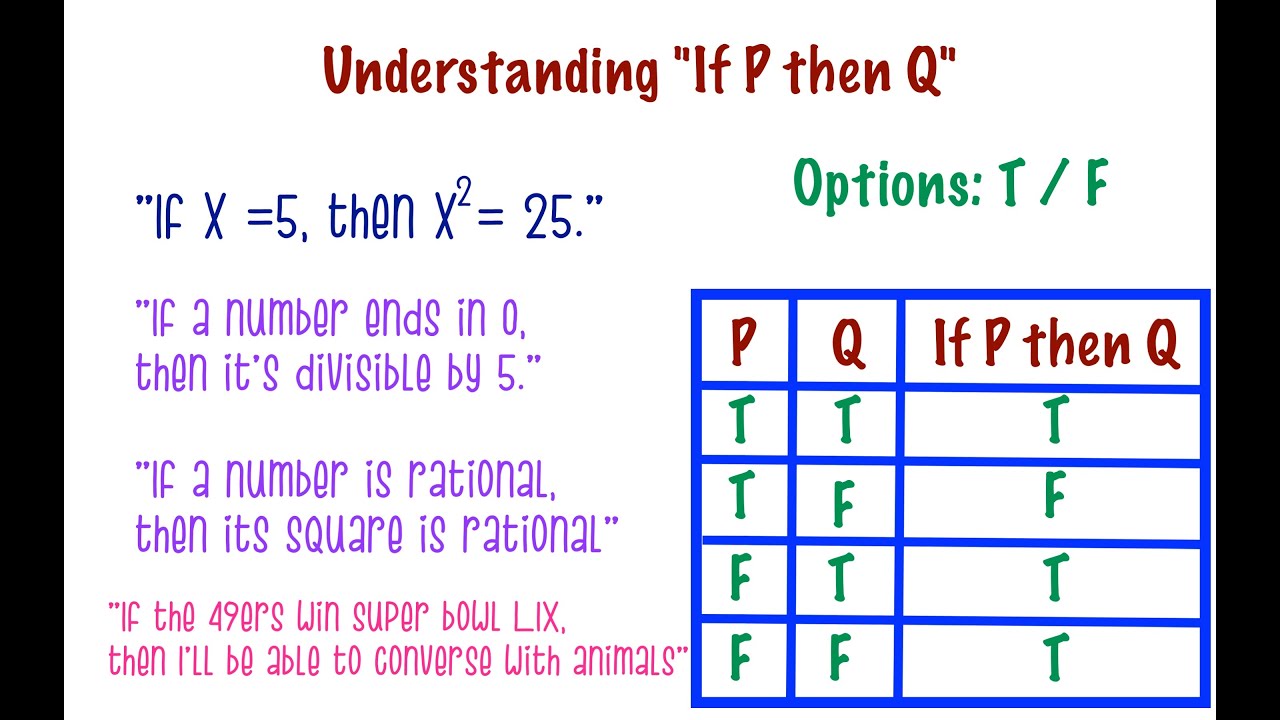
If P(x) Q(x) is true for some x, then P(x) is true for some x, or Q(x) is true for some x
If x p = x q = (xy) pq then show that p + q = 1-Find stepbystep Discrete math solutions and your answer to the following textbook question Use rules of inference to show that if ∀x(P (x) ∨ Q(x)) and ∀x((¬P (x) ∧ Q(x)) → R(x)) are true, then ∀x(¬R(x) → P (x)) is also true, where the domains of all quantifiers are the sameLearning Objectives1) Interpret sentences as being conditional statements2) Write the truth table for a conditional in its implication form3) Use truth tabl
If x p = x q = (xy) pq then show that p + q = 1のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  |  |
 |  | |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | ||
 | .png) | 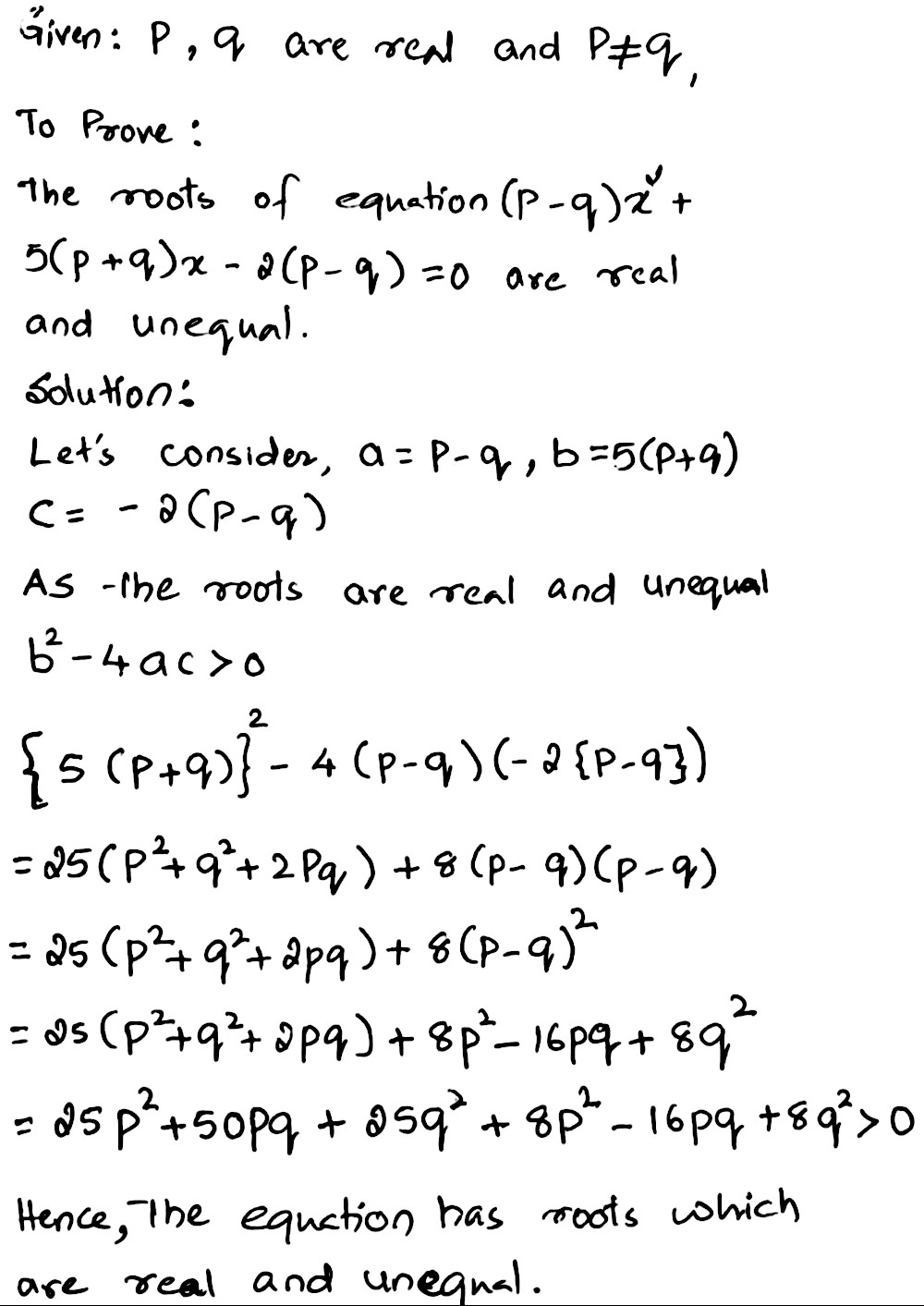 |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | 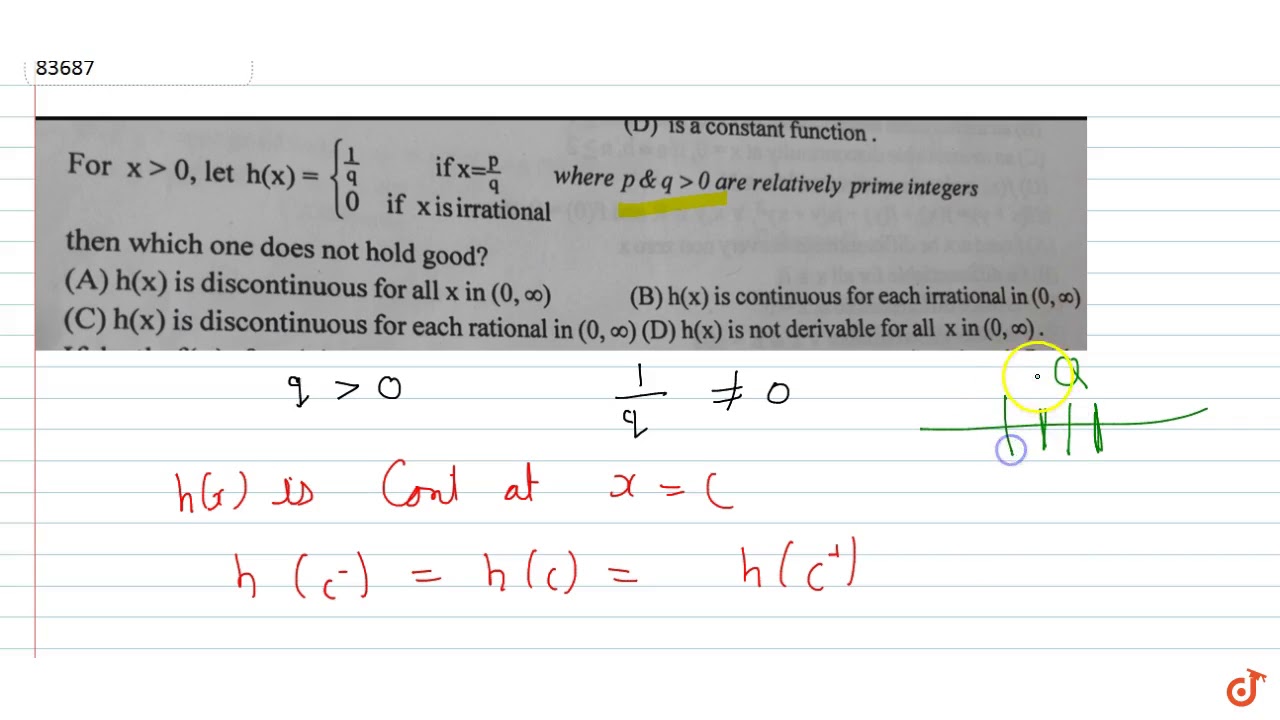 |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 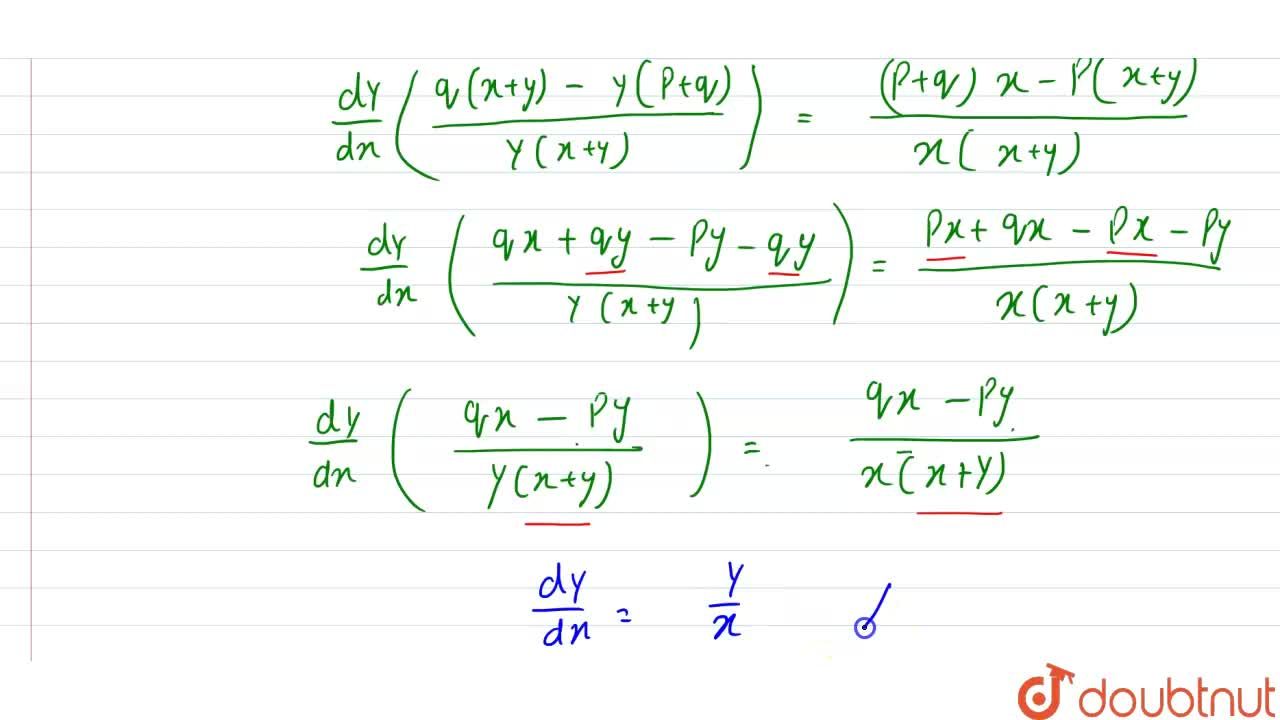 |
 |  |  |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
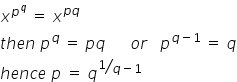 |  | |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  | |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 | ||
 |  | |
「If x p = x q = (xy) pq then show that p + q = 1」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
Therefore if p is true then q and r are true ∴ (¬p∨¬q) e negation ofP/Q 2 when simplified it comes in the form of (x1/x)3/(x1/x) then we can apply AM greater than or equal to GM we get the minimum value of p/q 2 as 2(3) 1/2
Incoming Term: if x^p^q=(x^p)^q then p=, if x^py^q=(x+y)^p+q then dy/dx, if x p = x q = (xy) pq then show that p + q = 1, if p q are coprime and hcf((p)/(q) (q)/(p))=(x)/(pq) then x=,




0 件のコメント:
コメントを投稿